We all more or less know how science works. Scientists make experiments and then write scientific articles to tell the world about their discoveries. In scientific journals, articles are reviewed by other scientists before being published to make sure the scientific method is properly followed. But should we always trust scientific articles? And if not, what scientific sources can we trust?
Why scientific experiments can go wrong

Randomness
In the real world, a lot of scientific experiments are made more complex by the presence of random phenomena. Consider dowsing for instance, which is the practice of finding water in the ground using an Y-shaped branch. Today, we know that dowsing does not work, because we have repeatedly tested it and found it to be inefficient. However, it has been believed to work for centuries. Why is that? When trying to find water, a dowser might find some “just by chance” so it’s hard to detect whether the dowser has a real talent or is just lucky. The proper mathematical tools to distinguish properly between the two cases have been developed only recently in history, in the 19th century.
Let’s imagine that we want to test if a dowser is able to find water. A possible experiment is to bury several pipes in the ground (this experiment has actually been done). In some, flowing water is sent, while others are kept empty. Let’s say for instance that there are 10 pipes and half of them contain water. Now a candidate dowser goes over each pipe and tries to tell if it contains water.
Let’s imagine that candidate #1 gives a correct answer only half of the time, then it is clear that he is a fraud because he does not do better than what is expected by chance. On the other hand, imagine that candidate #2 gets it right for all 10 pipes, it then seems credible that his talent is genuine. Candidate #3 gets it right 8 times, but makes 2 mistakes. Is his talent genuine then? It’s not obvious to tell…
Scientists have developed a mathematical tool to solve this problem. This is called a statistical test and it allows us to calculate the probability to find an “as good” result just by chance in the case the choice is made at random. Scientists call this probability a “p-value” (for Probability Value). If the observation is very unlikely to occur by chance, we can then say that the candidate dowser probably has a real talent. If the result is likely to occur by chance, it means that the dowser is a fraud (or to be more precise, that his talent is not good enough to be detected by a test of this small size). So what does it give us for our 3 candidates?
Candidate #1: Wrong half of the time => Probability to be that good by chance: 74% (very likely) => Obviously a fraud
Candidate #2: Correct all the time => Probability to be that good by chance: 0.4% (very unlikely) => Probably genuine talent
Candidate #3: Right for 8 pipes but 2 mistakes => Probability to be that good by chance: 10% (quite likely in fact) => It could be just by chance
How “unlikely” does a result need to be to convince scientists that a dowser has a genuine talent? The convention for statistical tests is to require a p-value lower than 5% or 1%. With this criterion, an article claiming that dowsing works based on a candidate that performs like #3 would be rejected by scientific journals as “not statistically significant”, while an article claiming dowsing works with a candidate like #2 could be published. Note that an article with results like candidate #1 or #3 could still be published as long as it does not conclude to have proven that dowsing works.
All this has an important implication: Some scientists are going to make false discoveries because of bad luck. Let’s say that a scientist does an experiment with a dowser and gets a perfect result like with candidate #2. The probability to get that by chance is 0.4% which is low enough for publication of an article, so it could be published. Even though a lucky guess with 0.4% chance seems very unlikely, it will happen on average for 0.4% of experiments. This means that if 1,000 experiments are made with dowsing, and even though dowsing does not actually work, around 40 experiments are going to get a perfect 10/10 score with their candidate and will claim to have proven that dowsing works. This phenomenon is not rare at all, because there are thousands of scientific articles published every day, so there are probably several articles per day which claim to discover things that are just the result of luck.
Conclusion: There are so many scientific publications that some will necessarily “be lucky” and claim to confirm hypotheses which are in fact false.
Other issues with scientific articles
We have explained above why scientists can sometimes make false discoveries because of bad luck. But other issues can lead to even more incorrect results published in (peer-reviewed) scientific journals:
Publication bias: Surprising discoveries are more interesting, so an article claiming that dowsing works (which is unexpected) is more likely to get published than an article finding that dowsing does not work, like hundreds of articles before. This is because scientific journals prefer “interesting” rather than “boring” results. A real-world example of this issue is that medical studies finding that a drug is efficient against a disease are more often published than those that find a drug to be inefficient.
Poor experiment design: If the experiment is not carefully controlled, some biases can lead to false discoveries. For instance, when testing drugs, telling patients whether they have a real drug or a placebo (a fake drug) will influence them, and lead to better recovery for those who think they have the real drug, even if it does not work at all (this is called “placebo effect”).
Dishonest statistical testing: Scientists often have a lot of pressure to publish many articles. Some are then tempted to cheat a little with statistical tests. For instance, with our dowsing test, imagine a scientist who offers several tries for a candidate, but mentions only the most successful result in the article, therefore underestimating the probability that this result can occur by chance.
Outright fraud: This is rare but it sometimes happens. Some scientists deliberately fabricate results that don’t correspond at all to real observations.

Why science works anyway
With all the problems I have exposed in the previous section, it might seem that science is completely flawed and that nothing it says can be trusted. However, I strongly believe we can in fact trust science, because there is a solution which allows us to overcome most of these problems: replication.
Replicating scientific results is a very important part of science. Even if an article is affected by one of the issues we mentioned, there is no reason for an independent lab to get the exact same issue. If an article accidentally (or fraudulently) finds that dowsing works, other scientists will find it interesting and try to contradict or confirm the discovery. Even if the original article has some issues, the new article is unlikely to have the same. Of course, the second article might be the incorrect one, so if two articles disagree, it might be interesting to do further research.
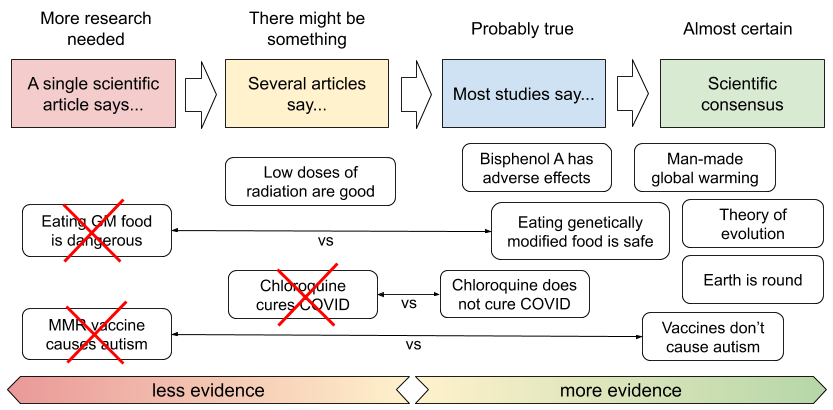
The important thing to remember is that you should never believe an hypothesis which is supported by a single scientific article. Doing otherwise can have terrible consequences. The controversy about vaccines causing autism emerged from a single fraudulent article published in 1998. The claimed link has not been found by new studies that tried to reproduce the results, so we are pretty sure now that there is no link between the MMR vaccine and autism. However, the media coverage of this article has led to a sharp drop in vaccination rates, leading to many avoidable deaths caused by the diseases the vaccine would have otherwise prevented.
More recently, a similar issue occured with the Séralini affair (2012). The article claimed that rats fed with genetically engineered maize treated with Roundup were more likely to develop tumors. The article was then criticized by other scientists as having done incorrect statistical testing, meaning that the results found a link which could easily have been the result of random chance. The article was then retracted, which means that the journal recognizes that it should not have published it. But the refutation and retractation were given much less news coverage, so the public mostly remembers the false discovery as being true and largely believes that eating genetically engineered food is dangerous, even though the scientific consensus considers them safe.
From article to consensus
For all the reasons we have explained earlier, a single scientific article can be wrong for many reasons. So are two articles enough? Well, it depends. If two articles find something which contradicts 50 other articles which have made the same experiment, their result is still likely to be false. However, if these are the only two articles making the experiment and they confirm each other, it might be a good indication that this is a good hypothesis.
When there are many articles on a single subject, it starts to be hard to see what is true because there are often several articles that contradict each other. For the reasons we have explained earlier, if thousands of articles exist on a single question, there are necessarily false discoveries among them. To see things clearly, scientists often write a special type of article, called a meta-analysis, which analyzes all the published articles, compares their methods, and concludes whether there is a clear consensus or not between them. This gives a good indication whether there is a scientific consensus.
The scientific consensus is the highest level of confidence that can be reached. It means that the theories have been repeatedly tested and are confirmed by many high-quality experiments. In the diagram below, I have tried to give a few examples of theories and how “sure” we are of them. Paradoxically, if you want to know about the scientific consensus on a subject, the best source is probably to look at Wikipedia (especially the English version which is reviewed a lot) because it has a policy of presenting things according to the scientific consensus (or saying that there is none if it is the case), and does a pretty good job at that.
Another alternative is to look at what official scientific institutions say, keeping in mind that a government can also be wrong for political reasons. But for instance, if both the CDC (US) and ECDC (EU) agree on something related to health, or the FDA and EFSA on something related to food, there is a good chance that they are conveying the scientific consensus. Again, Wikipedia might be useful to know whether there is a consensus between these institutions.
Conclusion
The scientific method is the most powerful tool mankind has ever created to discover things about the world it lives in. However, this does not mean that everything a scientific article says is automatically true. Science progresses by making a lot of mistakes along the way, but is able to overcome them by reproducing results several times. Scientific consensus appears when there is sufficient evidence that points in the same direction. It is the best level of certainty that can be reached by science and the best sign that something is almost certainly true.
No conflict of interest: The author of this article and this blog do not receive any money from, nor have any financial interests in the pharmaceutical, agrochemical or biotechnology industry.

For those interested in the calculation of the p-values, here is how I got them, using the R programming language:
> fisher.test(matrix(c(3,3,2,2), 2), alternative="greater")
Fisher's Exact Test for Count Data
data: matrix(c(3, 3, 2, 2), 2)
p-value = 0.7381
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
0.06479589 Inf
sample estimates:
odds ratio
1
> fisher.test(matrix(c(5,0,0,5), 2), alternative="greater")
Fisher's Exact Test for Count Data
data: matrix(c(5, 0, 0, 5), 2)
p-value = 0.003968
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
3.373109 Inf
sample estimates:
odds ratio
Inf
> fisher.test(matrix(c(4,1,1,4), 2), alternative="greater")
Fisher's Exact Test for Count Data
data: matrix(c(4, 1, 1, 4), 2)
p-value = 0.1032
alternative hypothesis: true…